Clustering data is the act of partitioning observations into groups, or clusters, such that each data point in the subset shares similar characteristics to its corresponding members. Cluster analysis is commonly used in fields that utilize data mining, pattern recognition and machine learning. While MATLAB has several clustering tools included in its arsenal, we’ll take a look at the function kmeans in this tutorial. Following classification of n observations into k clusters, we can use binary classification to investigate the sensitivity and specificity of our clustering.
Category Archives: Machine Learning
Clustering Part 1 – Binary Classification
Binary classification is the act of discriminating an item into one of two groups based on specified measures or variables. While previously we have discussed methods for determining values of logic gates using neural networks (Part 1 and Part 2), we will begin a series on clustering algorithms that can be performed in Matlab, including the use of k-means clustering and Gaussian Mixture Models. Prior to doing so, we will discuss how classification is evaluated, primarily through the discussion of sensitivity, specificity and the way to calculate these values through Matlab.
Neural Networks – A Multilayer Perceptron in Matlab
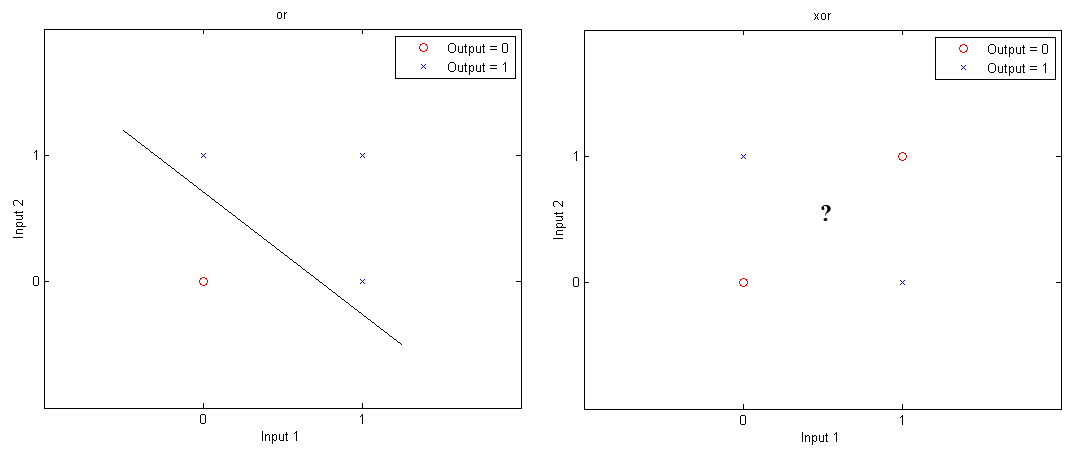
Previously, Matlab Geeks discussed a simple perceptron, which involves feed-forward learning based on two layers: inputs and outputs. Today we’re going to add a little more complexity by including a third layer, or a hidden layer into the network. A reason for doing so is based on the concept of linear separability. While logic gates like “OR”, “AND” or “NAND” can have 0’s and 1’s separated by a single line (or hyperplane in multiple dimensions), this linear separation is not possible for “XOR” (exclusive OR).
Neural Networks – A perceptron in Matlab
Neural networks can be used to determine relationships and patterns between inputs and outputs. A simple single layer feed forward neural network which has a to ability to learn and differentiate data sets is known as a perceptron.
By iteratively “learning” the weights, it is possible for the perceptron to find a solution to linearly separable data (data that can be separated by a hyperplane). In this example, we will run a simple perceptron to determine the solution to a 2-input OR.
Continue reading