A common problem in Matlab and every other programming language that uses floating point numbers is that calculations involving floats often do not yield the expected answers because of rounding, which can have undesirable effects on control statements. The immediate question is how to handle these rounding errors so that intuitively correct statements are recognized as true by a program. We would like to accomplish this while still retaining as much relevant information in the numbers as possible, thereby allowing the detection of minute differences that are not artifacts of rounding. In this post, some common errors in floating point comparisons will be discussed, as well as methods of handling these errors.
Relative Error Comparison
An example of a problematic floating point comparison is the addition or subtraction of two floating point numbers that should be equal to another floating point number, as demonstrated by the following commands.
>> A = 0.8 - 0.7; >> B = 0.1; >> A == B ans = 0 >> A - B ans = 8.32667268468867e-17
In this example, 0.8-0.7 should be equal to 0.1; however, their floating point representations are unequal because of rounding errors. A simple method to solve this problem would be to specify an acceptable level of error relative to the argument with the largest magnitude in the comparison. The following code shows how to implement this method in Matlab.
>> RE = 1e-12; >> abs(A-B) < RE*max(A,B) ans = 1
This method will work for arguments that are not very close to zero. The appropriate value of RE will vary based on the floating point precision (single or double) and the magnitude of the difference that is of interest. It is important to test various levels of RE in a program to determine what level will produce the desired results. In general, a value of 1e-6 for a double or 1e-3 for a single can be utilized if a somewhat large difference between the arguments is allowable. If the detection of minute differences is desired, then a value as low as 1e-12 or 1e-15 for a double or 1e-6 for a single could be used. Values of RE lower than this will most likely not yield correct answers for quantities that that are only separated by rounding error.
ULPS Comparison
A second method utilizes intimate knowledge of the floating point number format. Let’s take a closer look at the floating point representations of quantities A and B.
>> float2bin(A) ans = 0011111110111001100110011001100110011001100110011001100110100000 >> float2bin(B) ans = 0011111110111001100110011001100110011001100110011001100110011010
A and B differ by 6 ulps (units in the last place), which is equivalent to 6 × 2-4 × 2-52 = 3 × 2-55 = 8.33 × 10-17. One method to handle this would be to compare the difference between the two quantities with some multiple of the ulps of the quantity with the larger magnitude. In the following example, a factor of 32 is employed, which is approximately equivalent to RE = 1e-12, will reveal minute differences, and be an effective threshold in many situations.
>> A-B ans = 8.32667268468867e-17 >> abs(A-B) < 32*eps(max(A,B)) ans = 1
Both of these methods and the default comparison method were timed by executing repeated comparisons of the given values A and B for many repetitions. The first method completed 100,000 comparisons in approximately 3.06 s, and the second method completed the same number of comparisons in approximately 3.96 s. In contrast, the default comparison of A == B was executed 100,000 times in 0.370 s. Thus, there is a large penalty to pay for accuracy, but this may be acceptable depending on the requirements of the program. The second method, which uses eps, is roughly 30% slower than the first method, which uses relative error, but the second method allows the scaling of sensitivity in accordance with the actual structure of the number, which may be advantageous in some circumstances.
Comparisons for Results of Many Calculations
The two previously mentioned methods will work for a wide range of numbers with the exception of the infinities and NaNs. However, there is one important caveat: for a computation involving a large number of operations, the error will increase a great deal relative to the ulps of the result, often at a rate roughly proportional to the number of operations. For instance, look at the next example, which computes the following sum for increasing values of K:
>> format long >> K = 7; >> s = zeros(K,1); >> for k = 1:K > s(k) = sum((10^-k)*ones(10^k,1)); > end >> s ans = 1.000000000000000 1.000000000000001 1.000000000000001 0.999999999999906 0.999999999998084 1.000000000007918 0.999999999750170 >> e = abs(s - 1) e = 1.11022302462516e-16 6.66133814775094e-16 6.66133814775094e-16 9.38138455808257e-14 1.91624494050302e-12 7.91811061162662e-12 2.49830045540023e-10 >> e/eps(1) ans = 5.00000000000000e-01 3.00000000000000e+00 3.00000000000000e+00 4.22500000000000e+02 8.63000000000000e+03 3.56600000000000e+04 1.12513450000000e+06
This calculation completely overwhelms the factor of 32 used in our previous solution that utilized the ulps of the larger number in the comparison. If we assume that A = ∑ 10-K and B = 1, we would need a factor greater than 1.12 million for abs(A-B) < factor * eps(max(A,B)) to yield a value of true. Additionally, our calculation utilizing relative error would require a margin of 2.50e-10. Both of these methods require a margin for error that increases proportionally to the number of calculations. To manage the errors that result from these scenarios, one can multiply a basic relative error or ulps by the number of calculations. For instance, if the number of calculations is known to be N, use abs(A-B) < N*RE*max(A,B)) or abs(A-B) < N*factor*eps(max(A,B)). If the number of calculations is unknown, then an extremely high value such as N = 109 may be appropriate, as long as the comparison is remains sufficiently sensitive.
Comparisons with Zero
Comparisons of a number with zero are also quite problematic using floating point arithmetic. For example, consider the equation:
Performing this calculation using floating point numbers will yield a result that is close but not equal to zero. The following code shows the results for values of k varying from 1 to 7.
>> format short
>> K = 7;
>> t = zeros(K,1);
>> for k = 1:K
> t(k) = 1 + sum(-(10^-k)*ones(10^k,1));
> end
>> t
t =
1.1102e-16
-6.6613e-16
-6.6613e-16
9.3814e-14
1.9162e-12
-7.9181e-12
2.4983e-10
>> e = abs(t - 0);
>> u = arrayfun("eps", e); %Find eps(e) for every e
>> e/u
ans =
4.5036e+15
6.7554e+15
6.7554e+15
7.4327e+15
4.7444e+15
4.9011e+15
4.8324e+15
As shown above, comparisons with zero may yield results that are astronomically higher than their values of eps. Note that although sum t increases with the number of terms, the ratio of the sum to its value of eps does not vary substantially, staying within the same order of magnitude. Thus, even modest calculations can create problems for our comparison method if one of the arguments (A or B) is zero. If the ulps method were applied, a factor of 1e16 would be necessary to handle the errors, which would desensitize our comparison to the point of ignoring a great deal of information that may be of interest. If the comparison with zero cannot be avoided, the best way to solve this problem is to use an absolute comparison: abs(A-B) < abserr, where abserr could be a value such as 1e-6.
Conclusion
In summary, the best way to handle floating point rounding errors is to examine each comparison in your code and set a relative or absolute threshold based on the range of values that you expect in the arguments. For most numbers, a relative comparison will be adequate. For numbers that are the results of many calculations, a relative comparison with a much higher threshold may be appropriate. For comparisons with zero that cannot be avoided, an absolute threshold is recommended.
If a higher degree of sensitivity is required than what can be achieved using the techniques in this post, then other measures are necessary. If it is desirable to use Matlab, an extended precision format could be utilized. That is the approach used in this paper, in which the authors achieved an arbitrary precision format in Matlab by employing the ARPREC C++ library. Additionally, a different programming language that handles extended or arbitrary precision can be utilized. Languages such as C++, C#, Ruby, and Python all have arbitrary precision libraries.
This concludes our series on floating point numbers in Matlab. I hope that this series was useful and informative. If you are interested in more information about floating point numbers, I recommend the websites in the References section.
References
Great place to start for basics of floating point format
http://steve.hollasch.net/cgindex/coding/ieeefloat.html
Everything you ever wanted to know about floating point numbers (94 pages long)
http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
Comparisons of floating point numbers (I borrowed heavily from this site for this post)
http://randomascii.wordpress.com/2012/02/25/comparing-floating-point-numbers-2012-edition/
Has a good graphic that shows the distribution of floating point numbers
http://blogs.msdn.com/b/dwayneneed/archive/2010/05/07/fun-with-floating-point.aspx
Other Posts in Matlab Geeks Floating Point Number Series
Floating Point Numbers in Matlab
Conversion of Floating Point Numbers in Matlab
Conversion of Floating Point Numbers from Binary to Decimal

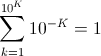
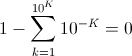
Note that your comparisons using relative error will not work when A and B are both negative. You want something like this:
>> RE = 1e-12;
>> abs(A-B) < RE*max(abs(A),abs(B))
how to know the absolute error for a double or floating number?
I see a lot of interesting articles on your website. You have to spend a lot
of time writing, i know how to save you a lot of time,
there is a tool that creates unique, google friendly posts in couple of minutes, just type in google – k2
unlimited content