The Fourier transform is one of the most useful mathematical tools for many fields of science and engineering. The Fourier transform has applications in signal processing, physics, communications, geology, astronomy, optics, and many other fields. This technique transforms a function or set of data from the time or sample domain to the frequency domain. This means that the Fourier transform can display the frequency components within a time series of data. The Discrete Fourier Transform (DFT) transforms discrete data from the sample domain to the frequency domain. The Fast Fourier Transform (FFT) is an efficient way to do the DFT, and there are many different algorithms to accomplish the FFT. Matlab uses the FFT to find the frequency components of a discrete signal.
The following is an example of how to use the FFT to analyze an audio file in Matlab. The file in this example is the recording of a tuning fork resonating at the note A4. This shows how the Fourier transform works and how to implement the technique in Matlab.
%Fourier Transform of Sound File
%Load File
file = 'C:\MATLAB7\work\tuning_fork_A4';
[y,Fs,bits] = wavread(file);
Nsamps = length(y);
t = (1/Fs)*(1:Nsamps) %Prepare time data for plot
%Do Fourier Transform
y_fft = abs(fft(y)); %Retain Magnitude
y_fft = y_fft(1:Nsamps/2); %Discard Half of Points
f = Fs*(0:Nsamps/2-1)/Nsamps; %Prepare freq data for plot
%Plot Sound File in Time Domain
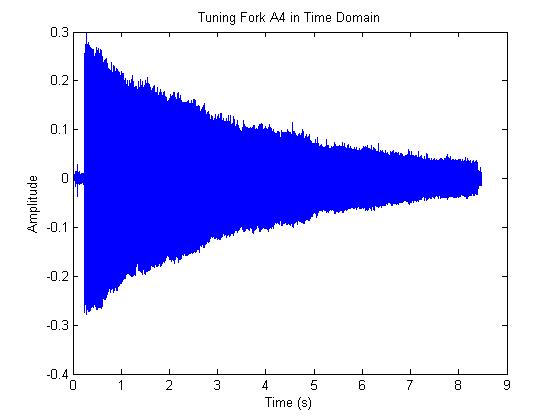
figure
plot(t, y)
xlabel('Time (s)')
ylabel('Amplitude')
title('Tuning Fork A4 in Time Domain')
%Plot Sound File in Frequency Domain
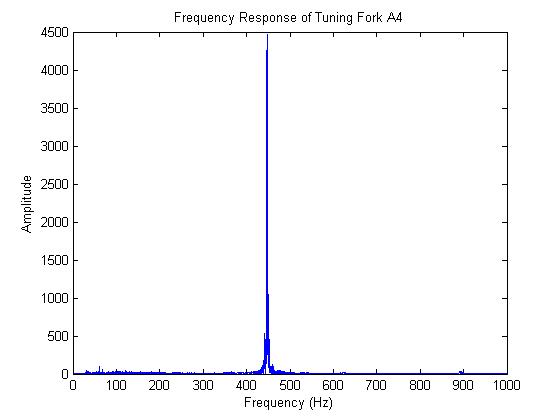
figure
plot(f, y_fft)
xlim([0 1000])
xlabel('Frequency (Hz)')
ylabel('Amplitude')
title('Frequency Response of Tuning Fork A4')
The sound file tuning_fork_A4 is opened using the wavread function, which returns the sampled data from the file, the sampling frequency, and the number of bits used in the A/D converter. Note that the file extension “.wav” does not have to be specified in the function call. The sampling frequency is important for interpreting the data, as shown below.
The FFT is performed using the “fft” function. Matlab has no “dft” function, as the FFT computes the DFT exactly. Only the magnitude of the FFT is saved, although the phase of the FFT is useful is some applications. The “fft” function allows the number of points outputted by the FFT to be specified, but for this example, we will use the same number of input and output points. In the next line, half of the points in the FFT are discarded. This is done for the purposes of this example, but for many applications, the entire spectrum is interesting. In the following line, the data that will be used for the abscissa is prepared by using the sampling frequency and the number of samples in the time domain. This step is important to determine the actual frequencies contained in the audio data.
Next, the original data are plotted in the time domain and the FFT of the data is plotted. The x-axis is limited to the range [0, 1000] in this plot to show more detail at the peak frequency. Notice that the frequency response contains a spike at approximately 440 Hz, which is the frequency of the note A4. There is also very little content at other frequencies, which is expected for a tuning fork. For other instruments, such as a guitar, harmonics at multiples of the peak frequency would be visible in the frequency response.
 The Fourier transform is a useful tool in many different fields. Two-dimensional Fourier transforms are often used for images as well. Try the code above for yourself to see if you can get the same results.
The Fourier transform is a useful tool in many different fields. Two-dimensional Fourier transforms are often used for images as well. Try the code above for yourself to see if you can get the same results.

How do you record the sound of tuning fork
What is the source that you relied on
need help with matlab code for generating fourier transform of m(t)=50sin(Wmt)
Then compare that plot as a function of t with the freq modulated signal of values of B between 1 & 20 : s(t)=cos[Bsin(Wmt)]
When the unit of the amplitude in time domain is bar(pressure), what is the unit of the amplitude in frequency domain?
how to get the minimum frequency and maximum frequency range of an audio signal.. i mean the range of audio signal in matlab?
already have the answer ?ialso looking for that
How do one remove the humming noise?
Thank you.
Hello,
Thanks for this article it’s very interesting.
I have learnt that when you want to remove background noise from a specific file we use fourier transform. For example I have a file with a continuous beeping sound. Suppose I want to remove the beeping sound from the file. What’s the procedure to follow?
Is there anyone know how to make time domain and frequency domain to have the same amplitude ?
Use Matlab to find Fourier transform of the following signals and also plot the spectrum with respect to w
.x(t)= 3[u(t−3)−u(t−7)]
Could anyone explain why it’s necessary to discard half of the points taken?
It initially seemed to be a way to save time processing data (I can see this being a problem for larger files), but it makes a huge difference in the frequency plot when I leave the step out.
Thanks!
Hi there, You’ve done an excellent job. I will certainly digg it and
personally recommend to my friends. I am sure
they’ll be benefited from this website.
I have a waveform and i need it’s fft. I don’t have the function of the waveform. I have x,y data.
how can i plot fft?
The Fourier Transform has always been a fascinating subject for me, and it is this excitement that leads me to present this Fourier Transform tutorial.
Is there any way that I can get an excel outlet instead of a graph?
thx
You will be required to carry out convolution between two digital signals and then find their Frequency Response (FFT). You may NOT use ‘conv’ function in Matlab however you may use the in-built Matlab function of ‘fft’ for calculating the frequency response.
A = [ 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1];
B = [ 0.309 0.587 0.809 0.951 1 0.951 0.809 0.587 0.309 1.224e-16 -0.309 -0.587 -0.809 -0.951 -1 -0.951 -0.809 -0.587 -0.309 -2.449e-16];
a) Find Frequency Response of following two Signals: b) Carry out convolution between ‘A’ and ‘B’ to get ‘C’. c) Find the frequency response of ‘C’
Provide the code
thnx
bakwas thak dia
actually I am working on IC engine vibration analysis.. a set of data points(2002000) is available..sampling frequency is 20000hz and recorded time is 100 sec..I want to obtain fft of the signal(data points: 500500,for 25 sec). I don’t know whether the coding is right or not, but can’t obtain the appropriate figure…please anybody help me out…
here’s the matlab code..
figure;
fs = 20020.0; % Sampling frequency
delt= 1.0/fs; % Sampling time interval
s= length(imf); % number of data points
s1=(s/2);
totaltime = s*delt; %length of the time signal
y=imf; % array(set of data points)
yfft=fft(y);
yabs=(abs(yfft));
delf=(1.0/totaltime);
n2 = 1:1:(s1);
fk=delf.*n2;
plot(fk,(yabs(1:s1)));
xlabel(‘Frequency (Hz)’)
ylabel(‘Amplitude’)
wtff
i have a project about fourier transform how can i do it ?
thx in advance
You can do it correctly or wrong for example.
hi,
i am trying to develop an algorithm for walsh hadamard fourier transform.
do anyone of you know about walsh hadamard fourier transform.
if so, please let me know
hi,
i am trying to develop an algorithm for walsh hadamard fourier transform.
do anyone of you know about walsh hadamard fourier transform.
if so, please let me know
I had been wondering if your hosting is OK? Not that I’m complaining, but slow loading instances times will sometimes affect your placement in google and can damage your quality score if ads and marketing with Adwords.
hello every one !
i m trying to design an AEC (acoustic echo canceller) !
but i m a complete novice ! i dont know how to find echo order? (they are 4 peaks when i use xcorr: so i guess its 3) ! and also i am unaware how to compute delays and attenuation factors!
i aspire to learn it from the basic. so i m not using built in echo canceller libraries in matlab!
please guide.
thanks
Hi,
What about the phase?? You just plot the amplitude of the transformed data. In other words, how can I use FFT to do fourier transform and retain information of both amplitude and phase ??
Thanks
find the discrete fourier transform of image with (.png)?
Hashem,
Please read this post on doing an FFT on an image.
https://matlabgeeks.com/tips-tutorials/how-to-do-a-2-d-fourier-transform-in-matlab/
Thanks,
Eric
I working on a project that using audible sound to detect cracked eggs.
The idea is that: excite a sound toward the egg, then record the feflecting sound, and to use FFT analyse it.
I am just at the begining of the project but got some difficulities with FFT.
It is not easy to explain here. So, may I know your email address? Then I send an report with more details and picture.
Thank you,
Le Duong Huy
Le Duong Huy,
I apologize for not answering sooner. I did not see the notification in WordPress. That sounds like an interesting project. Please send any questions to service@matlabgeeks.com or post in our forums.
Thanks,
Eric
Please send us the details-
thanks … for shear…
more helpful
Hey, which function can help me to calculating the “twiddle factors” in any points of FFT? Thank you
i am doing an android project for calculating the density on the road traffic. how do i analyse the sound gathered using android microphone using matlab?
please do give example how to replace the fft with the loop…*example of the matlab coding to replace fft…
Here is the Matlab code on how to do a Fourier Transform if you do not want to use FFT. You could also use vectorized code, but this should be easier to understand. The function fft will be much faster than the code below.
http://www.mathworks.com/help/techdoc/ref/fft.html
N = 10; //Length of vector
wn = exp(-2*pi*i/N); //Kernel
x = sin(2*pi*(0:N-1)); //Can be any function
X = zeros(1,N); //FFT of x
for k = 1:N
X(k) = 0;
for j = 1:N
X(k) = X(k) + x(j)*wn^((j-1)*(k-1));
end
end
Thank you very much for this piece of code. I have to give a course about this and made a stupid mistake. You saved my afternoon !
how will be the code be if we want to do circular convolution with fft in two dimension
hey there, i was wondering if anyone knew how to calculate the energy compaction in an image and also the percentage of the total image energy in a number of 10% of the lowest frequency coefficients. thanks
i have translate your post in indonesian at my blog, thanks
Please, I want to use all the points in the FFT but I’m not able to modify. Can you help me?
thanks
Pingback: How to do fft on matlab
how do you do it with out using the FFT function?
You could actually implement the Fourier transform formula by using a for loop. Mathworks gives the formula which produces a result that is identical to the FFT function: http://www.mathworks.com/help/techdoc/ref/fft.html
I guess I’m not sure why you would want to do that, since the FFT function works great.
hey buddy did you get the method to do fft without function…..?