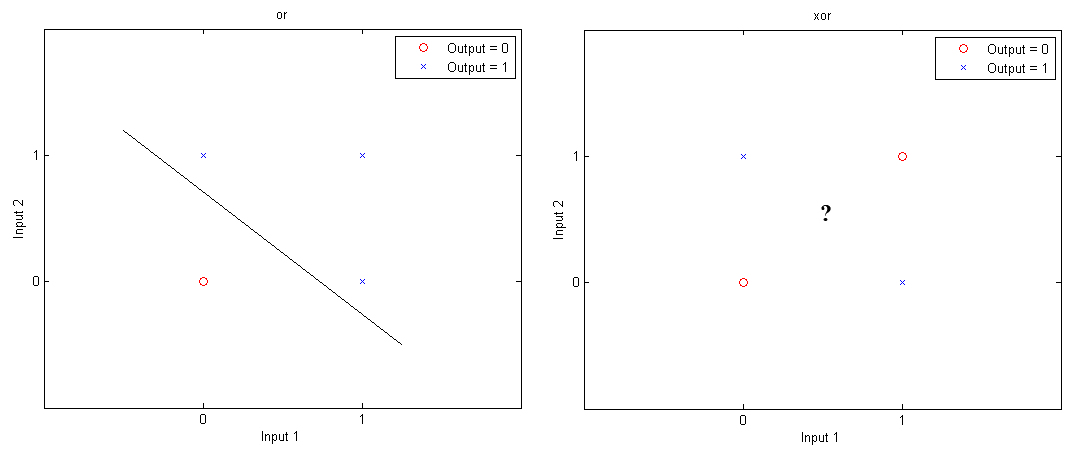
Previously, Matlab Geeks discussed a simple perceptron, which involves feed-forward learning based on two layers: inputs and outputs. Today we’re going to add a little more complexity by including a third layer, or a hidden layer into the network. A reason for doing so is based on the concept of linear separability. While logic gates like “OR”, “AND” or “NAND” can have 0’s and 1’s separated by a single line (or hyperplane in multiple dimensions), this linear separation is not possible for “XOR” (exclusive OR).
As the two images above demonstrate, a single line can separate values that return 1 and 0 for the “OR” gate, but no such line can be drawn for the “XOR” logic. Therefore, a simple perceptron cannot solve the XOR problem. What we need is a nonlinear means of solving this problem, and that is where multi-layer perceptrons can help.
First let’s initialize all of our variables, including the input, desired output, bias, learning coefficient, iterations and randomized weights.
% XOR input for x1 and x2
input = [0 0; 0 1; 1 0; 1 1];
% Desired output of XOR
output = [0;1;1;0];
% Initialize the bias
bias = [-1 -1 -1];
% Learning coefficient
coeff = 0.7;
% Number of learning iterations
iterations = 10000;
% Calculate weights randomly using seed.
rand('state',sum(100*clock));
weights = -1 +2.*rand(3,3);
Similar to biological neurons which are activated when a certain threshold is reached, we will once again use a sigmoid transfer function to provide a nonlinear activation of our neural network. As we mentioned in our previous lesson, the sigmoid function 1/(1+e^(-x)) will squash all values between the range of 0 and 1. Also a requirement of the function in multilayer perceptrons, which use backpropagation to learn, is that this sigmoid activation function is continuously differentiable.
Lets set up our network to have 5 total neurons (if you are interested you can change the number of hidden nodes, change the learning rate, change the learning algorithm, change the activation functions as needed. In fact the artificial neural network toolbox in Matlab allows you to modify all these as well.)
This is how the network will look like, with the subscript numbers utilized as indexing in the Matlab code as well.
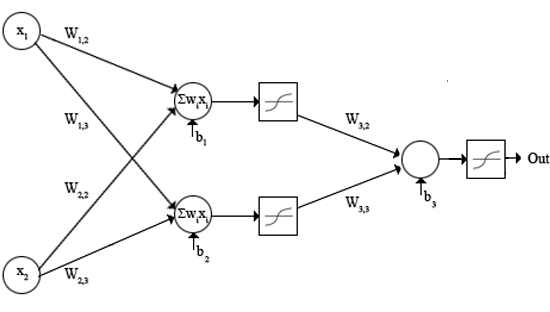
Whereas before we stated the delta rule as delta = (desired out)-(network output), we will use a modification, which is nicely explained by generation5 .
Back-propagation with the delta rule will allow us to modify the weights at each node in the network based on the error at the current level n and at the n+1 level.
Now for the code with back propagation.
for i = 1:iterations
out = zeros(4,1);
numIn = length (input(:,1));
for j = 1:numIn
% Hidden layer
H1 = bias(1,1)*weights(1,1)
+ input(j,1)*weights(1,2)
+ input(j,2)*weights(1,3);
% Send data through sigmoid function 1/1+e^-x
% Note that sigma is a different m file
% that I created to run this operation
x2(1) = sigma(H1);
H2 = bias(1,2)*weights(2,1)
+ input(j,1)*weights(2,2)
+ input(j,2)*weights(2,3);
x2(2) = sigma(H2);
% Output layer
x3_1 = bias(1,3)*weights(3,1)
+ x2(1)*weights(3,2)
+ x2(2)*weights(3,3);
out(j) = sigma(x3_1);
% Adjust delta values of weights
% For output layer:
% delta(wi) = xi*delta,
% delta = (1-actual output)*(desired output - actual output)
delta3_1 = out(j)*(1-out(j))*(output(j)-out(j));
% Propagate the delta backwards into hidden layers
delta2_1 = x2(1)*(1-x2(1))*weights(3,2)*delta3_1;
delta2_2 = x2(2)*(1-x2(2))*weights(3,3)*delta3_1;
% Add weight changes to original weights
% And use the new weights to repeat process.
% delta weight = coeff*x*delta
for k = 1:3
if k == 1 % Bias cases
weights(1,k) = weights(1,k) + coeff*bias(1,1)*delta2_1;
weights(2,k) = weights(2,k) + coeff*bias(1,2)*delta2_2;
weights(3,k) = weights(3,k) + coeff*bias(1,3)*delta3_1;
else % When k=2 or 3 input cases to neurons
weights(1,k) = weights(1,k) + coeff*input(j,1)*delta2_1;
weights(2,k) = weights(2,k) + coeff*input(j,2)*delta2_2;
weights(3,k) = weights(3,k) + coeff*x2(k-1)*delta3_1;
end
end
end
end
Try to go through each step individually, and there are some additionally great tutorials online, including the generation5 website.
As for the final results?
Well the Weights are:
weights =
-9.8050 -6.0907 -7.0623
-2.4839 -5.3249 -6.9537
5.7278 12.1571 -12.8941
These weights represent just one possible solution to this problem, but based on these results, what is the output? Drumroll please…
out =
0.0042
0.9961
0.9956
0.0049
Not bad, as the expected is [0; 1; 1; 0], which gives us a mean squared error (MSE) of 1.89*10^-5. Of course we ran this using 100,000 iterations, and while this could be optimized further, stopped earlier modified to have different architecture as mentioned previously, I’ll leave that to you or for a further lesson down the road.

There is a mistake in the calculation of weights (input-to-hidden). The lines that read:
weights(1,k) = weights(1,k) + coeff*input(j,1)*delta2_1;
weights(2,k) = weights(2,k) + coeff*input(j,2)*delta2_2;
should be corrected to
… = … + coeff*input(j,k-1)*delta2_1;
… = … + coeff*input(j,k-1)*delta2_2;
Nevertheless, great example!
yes there is weight update problem, I saw that too..
but, when I change it to your code (or any correct calculation I assume) it fails and gives incorrect results.
Don’t rally know why!!!
Any one?
Please re-arrange the block diagram of the neural network because w_22 and w_13 are misplaced at the figure.
Does anyone know how I can plot the classification line? The classification line shown in the diagram, in the beginning of the post, I want to know how to plot it. Does anyone know how to do it?
how can i back the values
0.0042
0.9961
0.9956
0.0049
to
0
1
1
0
i mean when test another sample why 0.0049 is rounded to 0 it may be 1
Generally, anything below 0.1 is taken to be 0 and anything above 0.9 is taken to be 1 because you cant have complete convergence.
Hi Everyone
please do me a favour. i want to know how i classify Fisheriris dateset (default dataset of matlab) with multilayer perceptron using Matlab. I implement MLP for xor problem it works fine but for classification i dont know how to do it….
Thanx in Advance
Hello there,
tried the code and got
out =
0.4995
0.4777
0.5005
0.5223
Any help ?
I checked this code for I need a similar project with two inputs and 5 hidden layers to one output..
Thank you
You should use “logsig” instead of “sigma’.
i use logsig instead of sigma…but result is same…pls suggest…will i other activation function for this to get result which is close to target..i want the result same as you..pls tell how can i use sigma?
thank you..find the problem..pls look the problematic part here..
write H1,H2 and X3_1 in one line
and use sigmoid function like below:
x2(1) = 1/(1+exp(-H1));
I am looking for artificial metaplasticity on multi-layer perceptron and backpropagation. Is there possibility to help me to write an incremental multilayer perceptron matlab code
thank you
I am looking for artificial metaplasticity on multi-layer perceptron and backpropagation for prediction of diabetes. Is there possibility to help me to write an incremental multilayer perceptron matlab code
thank you
I am looking for artificial metaplasticity on multi-layer perceptron and backpropagation. Is there possibility to help me to write an incremental multilayer perceptron matlab code
thank you
Hi, thank you for the code ,but result isn’t correct as you had it.
Could you please explain where is the problem ???
thanks
it might be that it is missing a threshold value like 0.7. What i mean by this is you would need to 0.7 in the equation H1 = ((bias(1,1)*weight(1,1))-threshold)+((input(j,1)*weight(1,2))-threshold) … so on and on
Hello
Neural network with three layers,11 neurons in the input , 1 neurons in output ,4 neurons in the hidden layer , Training back- propagation algorithm , Multi-Layer Perceptron Please , help me
Send to Email
plz can any one send me the correct code XOR where i can use the user defined function as i have to use different nonlinear function for my network
i tried the above mentioned code but they are not working for me
the EX-OR code is ok but when i try to add my function i get error signal my function is simply tanh function with some addition components
thanks
Thoughtful suggestions – Just to add my thoughts , if someone is searching for a CA SUM-100 , my assistant came across a template version here
https://goo.gl/IMGWAK.Hello
Neural network with three layers, 2 neurons in the input , 2 neurons in output , 5 to 7 neurons in the hidden layer , Training back- propagation algorithm , Multi-Layer Perceptron . input ‘xlsx’ with 2 column , 752 .
Please , help me
Send to Email
can anyone mail me the matlab code without using toolbox for speech recognition using neural networks
can anyone mail me the matlab code without using toolbox for speech recognition using toolbox
Hi,
I try your code but I didn’t find the same result.
I found 0.4995 0.4777 0.5005 0.5223 as output.
I replaced sigma by 1/(1+exp(X) for the Hidden and output layer .
Somebody have the solution?
Hi there! Tried my self replacing the sigma function for 1/(1+exp(-X)) and it worked fine. I believe you may have forgotten the minus sign in one of the functions, please check your code.
Good luck.
hello i tried this code and i find a bad results. Can any one help me to solve my problem
The problem that I found is this part “H2 = bias(1,2)*weights(2,1)
+ input(j,1)*weights(2,2)
+ input(j,2)*weights(2,3);”
If you copy the program straight from this website and put it in the matlab the calculation will not work properly. It only calculates H2 = bias(1,2)*weights(2,1) and assumes the next lines are a part of a new calculation. So what you need to do is write out the equation in one line “H2 =bias(1,2)*weights(2,1) +input(j,1)*weights(2,2) +input(j,2)*weights(2,3);”
This applies to other similar commands as well.
% XOR input for x1 and x2
input = [0 0; 0 1; 1 0; 1 1];
% Desired output of XOR
output = [0;1;1;0];
% Initialize the bias
bias = [1 1 1];
% Learning coefficient
coeff = 0.7;
% Number of learning iterations
iterations = 10000;
% Calculate weights randomly using seed.
rand(‘state’,sum(100*clock));
weights = -1 +2.*rand(3,3);
for i = 1:iterations
out = zeros(4,1);
numIn = length (input(:,1));
for j = 1:numIn
% Hidden layer
H1 = bias(1,1)*weights(1,1)
+ input(j,1)*weights(1,2)
+ input(j,2)*weights(1,3);
% Send data through sigmoid function 1/1+e^-x
% Note that sigma is a different m file
% that I created to run this operation
x2(1) = sigmf(H1,[1 0]);
H2 = bias(1,2)*weights(2,1);
H2 = bias(1,2)*weights(2,1)
+ input(j,1)*weights(2,2)
+ input(j,2)*weights(2,3);
x2(2) = sigmf(H2,[1 0]);
% Output layer
x3_1 = bias(1,3)*weights(3,1)
+ x2(1)*weights(3,2)
+ x2(2)*weights(3,3);
out(j) = sigmf(x3_1,[1 0]);
% Adjust delta values of weights
% For output layer:
% delta(wi) = xi*delta,
% delta = (1-actual output)*(desired output – actual output)
delta3_1 = out(j)*(1-out(j))*(output(j)-out(j));
% Propagate the delta backwards into hidden layers
delta2_1 = x2(1)*(1-x2(1))*weights(3,2)*delta3_1;
delta2_2 = x2(2)*(1-x2(2))*weights(3,3)*delta3_1;
% Add weight changes to original weights
% And use the new weights to repeat process.
% delta weight = coeff*x*delta
for k = 1:3
if k == 1 % Bias cases
weights(1,k) = weights(1,k) + coeff*bias(1,1)*delta2_1;
weights(2,k) = weights(2,k) + coeff*bias(1,2)*delta2_2;
weights(3,k) = weights(3,k) + coeff*bias(1,3)*delta3_1;
else % When k=2 or 3 input cases to neurons
weights(1,k) = weights(1,k) + coeff*input(j,1)*delta2_1;
weights(2,k) = weights(2,k) + coeff*input(j,2)*delta2_2;
weights(3,k) = weights(3,k) + coeff*x2(k-1)*delta3_1;
end
end
end
end
hi all . please help me
i need to solving xor problem with p-delta (parallel perceptron) in matlab . any one can help me ?
hi, like
tanks 😉
Hello.
I need to doCategory MLP on the images of MRI .
I know a little of MLP.
I do not know how it would implement on my images.
Can someone help me?
Regard.
sorry.
I need to do MLP on the images of MRI .
I know a little of MLP.
I do not know how it would implement on my images.
Can someone help me?
Regard.
How can we use different activation function for the same MATLAB code for example Elliot Symmetric activation function to remove the requirement of exponent part?
hi i need matlab code for integrte pso based on bp neural network please help me
hi
i want to write code for xor with learn p
please help
thank you
Is it right delta = (1-actual output)*(desired output – actual output) ?
I have a doubt about the factor (1-actual output) multiplied on (desired output – actual output).
hello i have recently started working on artificial neural network in matlab . i’m having some trouble in creating a program to calculate natural frequency of a plate using mlp and back propogation
PLZ help??
Hi
, I want to use “nntool”, the GUI function to create a GRNN network and train it. But I find that the train button is blocked. When I use feed-forward backprop to create the work, it seems work it again. Can you tell me why?
it is based on unsupervised learning thats why train button does not work u can only simulate the network created before
There’s a mistake in the code. weight coefficients are mixed up. According to the picture the coefficients weight(1,3) and weight(2,2) (in H1 and H2 calculations) should be replaced. The weight updating calculations are correct according to the picture.
pleas i need matlab code to separate 16 class like as QAM 16 thanks .
hello,
your code looks very interesting and works. However there is a question: where in the code does it state that there will be 5 hidden nodes? or how many hidden neuron?
thank you.
sabrina
I need help with writing code for neural network 2-layer architecture for XOR function. Can I email you my code and you can guide me please.
hi dear
how can i implement a back propagation algorithm in matlab without neural network toolbox
and our input are matrices with variant dimension
more over a curve for error
best wish
hi
Does anybody have experience setting the transfer function to be a linear equation instead of a sigma, tanh etc. The final solution can be linearly regressed to produce a multiple linear regression equation – which is a much cleaner output. Effectively, you can exploit the robustness of ANN learning to fit a multiple linear equation rather least squares (which is highly sensitive to outliers). Naturally, this should only be used when the expected output can modelled using MLR.
hi
i need your help!!!!
how can i found out use perceptron with one layer or multi layers for solving a problem
Hello Sir,
I just need the code for Multilayer Perceptron feed forward network.
i need a script on matlab using the multilayer perceptron in predection , thank you
%Created by Arghya Pal
%Date 09/03/2014
%M.Tech, Goa University
% a program for back propagation network for EX-OR gate
%Machine Learning
close all, clear all, clc
x = [0 0 1 1; 0 1 0 1]
t = [0 1 1 0]
[ni N] = size(x)
[no N] = size(t)
nh = 2
% wih = .1*ones(nh,ni+1);
% who = .1*ones(no,nh+1);
wih = 0.01*randn(nh,ni+1);
who = 0.01*randn(no,nh+1);
c = 0;
while(c < 3000)
c = c+1;
% %for i = 1:length(x(1,:))
for i = 1:N
for j = 1:nh
netj(j) = wih(j,1:end-1)*x(:,i)+wih(j,end);
% %outj(j) = 1./(1+exp(-netj(j)));
outj(j) = tansig(netj(j));
end
% hidden to output layer
for k = 1:no
netk(k) = who(k,1:end-1)*outj' + who(k,end);
outk(k) = 1./(1+exp(-netk(k)));
delk(k) = outk(k)*(1-outk(k))*(t(k,i)-outk(k));
end
% back propagation
for j = 1:nh
s=0;
for k = 1:no
s = s + who(k,j)*delk(k);
end
delj(j) = outj(j)*(1-outj(j))*s;
% %s=0;
end
for k = 1:no
for l = 1:nh
who(k,l) = who(k,l)+.5*delk(k)*outj(l);
end
who(k,l+1) = who(k,l+1)+1*delk(k)*1;
end
for j = 1:nh
for ii = 1:ni
wih(j,ii) = wih(j,ii)+.5*delj(j)*x(ii,i);
end
wih(j,ii+1) = wih(j,ii+1)+1*delj(j)*1;
end
end
end
h = tansig(wih*[x;ones(1,N)])
y = logsig(who*[h;ones(1,N)])
e = t-round(y)
hi,pleaze
i neede source code matlab neural network MLP for character recognition.
i neede source code matlabe backpropagation.
size character input is 5*7
pleaze me help
mr30
%Created by Arghya Pal
%Date 09/03/2014
%M.Tech, Goa University
% a program for back propagation network for EX-OR gate
%Machine Learning
close all, clear all, clc
x = [0 0 1 1; 0 1 0 1]
t = [0 1 1 0]
[ni N] = size(x)
[no N] = size(t)
nh = 2
% wih = .1*ones(nh,ni+1);
% who = .1*ones(no,nh+1);
wih = 0.01*randn(nh,ni+1);
who = 0.01*randn(no,nh+1);
c = 0;
while(c < 3000)
c = c+1;
% %for i = 1:length(x(1,:))
for i = 1:N
for j = 1:nh
netj(j) = wih(j,1:end-1)*x(:,i)+wih(j,end);
% %outj(j) = 1./(1+exp(-netj(j)));
outj(j) = tansig(netj(j));
end
% hidden to output layer
for k = 1:no
netk(k) = who(k,1:end-1)*outj' + who(k,end);
outk(k) = 1./(1+exp(-netk(k)));
delk(k) = outk(k)*(1-outk(k))*(t(k,i)-outk(k));
end
% back propagation
for j = 1:nh
s=0;
for k = 1:no
s = s + who(k,j)*delk(k);
end
delj(j) = outj(j)*(1-outj(j))*s;
% %s=0;
end
for k = 1:no
for l = 1:nh
who(k,l) = who(k,l)+.5*delk(k)*outj(l);
end
who(k,l+1) = who(k,l+1)+1*delk(k)*1;
end
for j = 1:nh
for ii = 1:ni
wih(j,ii) = wih(j,ii)+.5*delj(j)*x(ii,i);
end
wih(j,ii+1) = wih(j,ii+1)+1*delj(j)*1;
end
end
end
h = tansig(wih*[x;ones(1,N)])
y = logsig(who*[h;ones(1,N)])
e = t-round(y)
and also i want to know what the function of this line:
rand(‘state’,sum(100*clock));
it was very good. but i think a book that after calculating the delta3_1 it goes toward weight and after that calculate the delta2_1 and delta2_2
are ther both of them corect or not??
Hi,
I also get these values for the output, instead of the expected ones.
0.499524196804705
0.477684866785518
0.500475803195295
0.522315133214482
I replaced sigma by x2(1) = 1/(1+exp(-x)); as everyone else did. Any suggestions? Is it possible to mail me the sigma.m file to rerun the code.Good work and thanks in advance
just change the bias to [1 1 1] you will get good results
The result is still bad after changing the bias from [-1 -1 -1] to [1 1 1]. 0.499524196804705
0.477684866785518
0.500475803195295
0.522315133214482
switch iterations from 10000 to 100000 and you will get output specified
I get the same results as George and Lyra – changing the bias and iterations does not change the output. Has anyone found what is wrong with the code?
make sure the similar equations
x3_1 = bias(1,3)*weights(3,1)+ x2(1)*weights(3,2)+ x2(2)*weights(3,3);
for H1 and H2 as well fit on a single line in matlab.
There seems to be an issue with them calculating properly if they are continued to the next line.
I am getting the same bad results: [ 0.4995 0.4777 0.5005 0.5223].
It makes no difference whether I use bias of -1 or 1.
I do not understand the comments about H1 and H2. The codes are as follows:
H1 = bias(1,1)*weights(1,1)
+ input(j,1)*weights(1,2)
+ input(j,2)*weights(1,3);
H2 = bias(1,2)*weights(2,1)
+ input(j,1)*weights(2,2)
+ input(j,2)*weights(2,3);
I can’t see anything wrong. Has someone tried to run the code posted here and succeeded?
can you please email me the sigma.m too ? Thank you.. 🙂
Puri_00211@yahoo.co.id
can you please email me the sigma.m too ? Thank you.. 🙂
function [ y ] = sigma( x )
y=1/(1+exp(-x));
end
The result is still bad after changing the bias from [-1 -1 -1] to [1 1 1]. 0.499524196804705
0.477684866785518
0.500475803195295
0.522315133214482
change iterations from 10000 to 100000 and you will get shown output above.
This doesn’t work – you still get the same bad results?
good work..
it helps me a lot if u post sigma.m file.
Bravo! Good approach.
But you forgot something to attach, that makes your work incomplete. Can you add here or send me the sigma.m file? Then I can have a look.
hi,please can you send me the sigma.m ?
thank you a lot for your program it works well, i want to use a linear function in the out node but when i integrate th purelin function or my own linear function the execution fail and i have nan nan nan in out if you can help me for this problem i’m waiting your answer
thanks
Write the pseudocode of an Multi-Layer Perceptron (NN) with Back-Propagation Learning algorithm
Hi,
I am user of artificial neural nets, I am looking for multi-layer perceptron and backpropagation. Is there possibility to help me to write an incremental multilayer perceptron matlab code
thank you
Hi,
I am user of neural nets, I am looking for backpropagation with incremental or stochastic mode, Is there possibility to help me to write an incremental multilayer perceptron matlab code for input/output regression
thank you
Hi,
I am user of neural nets, I am looking for backpropagation with incremental or stochastic mode, Is there possibility to help me to write an incremental multilayer perceptron matlab code
thank you
I’m trying to adapt this code to work in a character recognition program. A letter is converted to a binary array of 1’s and 0’s. The dimensions are 1×100. I have 4 letters that I would like to train the network to recognize. So the size of input would be 4×100. How can I adapt the code to work for my input size? Also, I would like the network to get trained so that the output is 1 2 3 4 instead of a 0 or 1 like your code does.
hey when i try to plot the error curve,i get 2 curves .. y is that .please help
This is very informative and thanks a lot. What if I want to just evolve a neural network to approximate a function. I dont want to train or use backpropagation, just a straight forward evolution of a nueral network. I understand that soem people call it NeuroEvolution.
Thanks in advance
I am very new in neural network.how can i train the network.how can i use the codes?
I am very new in neural network.how can I train a network?how can I use the codes?
Hey ,
Thanks for the tutorial. How can this be applied for stock market data fetched with y=yahoo ?
thax mate
hi…nice work but first as i read in the previous comments the scheme differ than the code& the answer is not c correct for me
0.499524196804705
0.477684866785518
0.500475803195295
0.522315133214482
this the out value idk why????
i replaced sigma by x2(1) = 1/(1+exp(-H1));
thx in advanced
Hi,
thanks for the tutorial, but how to implementation matlab program MLP NN to analisis Network Intrusion detection System with input Protocol ID, DNS, Source MAC,Source IP, Source Port, Dest MAC, Dest IP, Dest Port, ICMP type, ICMP Code, Raw Data Length, Raw Data Size and Output Attac or Not Attack and how to build hiden layer for that…. Thks
I seem to have the same problem as Don as well. The output is converging to 0.5;0.5;0.5;0.5 instead of 0;1;1;0. I use the exact code as posted above, but replaced the sigma function
function x = sigma(net)
x = 1/(1+exp(-net));
end
hi behnaz, i think i have found a problem in the backpropagation part of this code. I havent received any replies from the site admin to a few of my questions but reply to this if you want to collaborate! 🙂 cheers Jonathan
hi,
where is the problem please
can you please email me the sigma.m? Thank you..
can you please email me the sigma.m too ? Thank you..
amini_r89@yahoo.com
please sed me to my e-mail: im.marza@gmail.com
the code: sigma.m
Hi,
thanks for the intro to MLP’s and the example code – its been very helpful.
Out of interest, if I am building a net to predict, say efficiency of a component (in percent i.e. 0 – 100%) based of input parameters, how would I change the code to allow for outputs greater that the standard range [0 1] (for the sigmoid function)?
In other words, all the examples i have seen so far, give an output of either 0 or 1 or a value inbetween, but cannot give outputs outside of this range.
Kind regards
Jonathan
Jonathan,
Have you figure out how to get values outside of [0 1]? I was thinking of scaling down the output values by the maximum number in outputs. So if I have [1 2 3 4], new outputs would be [.25 .5 .75 1].
Please i was told to go and look what sigma means and its value,can you help me
Hi
Could you mail me the sigma.m?Thank you!
Hi,
Thanx for code, it’s cool. But I have problems with “weights=…” and “out=…”, I just can’t see it. Could u pls help me, it’s really urgent since I have an exam in few days.
When I run the code, it looks like this
H1 =
-2.7332
ans =
-0.8847
H2 =
-2.6884
ans =
-3.3642
x3_1 =
0.0019
ans =
-0.0041
H1 =
-2.7336
ans =
-0.8851
H2 =
-2.6884
ans =
-3.3642
x3_1 =
0.0893
ans =
and so on…((
if you type your code like this your problem would be solved:
H1 = bias(1,1)*weights(1,1) + input(j,1)*weights(1,2) + input(j,2)*weights(1,3);
(type in one line)
Hi Farzad Vasheghani,
Thanks, when i type in one line, the algorithm works!.
I have a question just for curiosity. Which is the problem of not type in one line?
sir,
i need the code for back propagation
How could I divide with 2 lines? 4 data sets?
Thank you in advanced!
Hi . This is good explanation of MLPNN . I have some problem in my code. I have a matrix of 30×11 and i want to classify this in three categories in 2-d plane . In this way i trained 60% data 10% validate and 30% for test. The three categories are
1- x<-1 -1<y<1
2- 01.8 y>0
3- x0
how can this achieve by MLPNN.
Hello there I am so grateful I found your website, I really found you by accident, while I was browsing on Askjeeve for something else, Regardless I am here now and would just like to say kudos for a remarkable post and a all round enjoyable blog (I also love the theme/design), I don�t have time to browse it all at the moment but I have book-marked it and also added in your RSS feeds, so when I have time I will be back to read much more, Please do keep up the superb job.
Hello, I don’t really understand why the weight matrix has 9 values in it. There are 6 in the diagram, are there not? I’m trying to figure out how to create a 4-input hidden layer but I am having difficulty understanding how the weights are derived within the code.
There is a weight applied to each of the 3 biases: 4 Input layer weights, 2 hidden layer weights, and 3 bias weights.
i also didn’t get it. why do you need to initiate a 3X3 matrix for the random weights? Was that supposed to be for the 3 biases?
so for any NN i’ll make that has 3biases? i’ll always have a 3X3matrix for the weight?
so for any NN i’ll make that has 3biases, i should always have a 3X3matrix for the randomized weights?
Hi.
I had recently try your network. Even if i had set the iteration to 100,000 times, the result is still far from the target values. I also try with shorter and larger iteration times to reconfirm the result. It seems that the error that propagate back to the network is not working very well as i am getting a similar results even with different iteration times. I hope you can revise it back or I am the only one have this problem??. FYI i am using Matlab 2010b.
Thanks.
I believe you’re the only one having problem. It works fine over here. You may want to;
clear all; close all; clc
then copy and paste code to try it again.
Hi,
I am a newby when it comes to ANNs, but your site has been of great help! However, I seem to have the same problem as Don as well. The output is converging to 0.5;0.5;0.5;0.5 instead of 0;1;1;0. I use the exact code as posted above, but replaced the sigma function as suggested by Vipul. Here is the code I am using:
input = [0 0; 0 1; 1 0; 1 1];
% Desired output of XOR
output = [0;1;1;0];
% Initialize the bias
bias = [-1 -1 -1];
% Learning coefficient
coeff = 0.7;
% Number of learning iterations
iterations = 10000;
% Calculate weights randomly using seed.
rand(‘state’,sum(100*clock));
weights = -1 +2.*rand(3,3);
for i = 1:iterations
out = zeros(4,1);
numIn = length (input(:,1));
for j = 1:numIn
% Hidden layer
H1 = bias(1,1)*weights(1,1)
+ input(j,1)*weights(1,2)
+ input(j,2)*weights(1,3);
% Send data through sigmoid function 1/1+e^-x
% Note that sigma is a different m file
% that I created to run this operation
x2(1) = 1/(1+exp(-H1));
H2 = bias(1,2)*weights(2,1)
+ input(j,1)*weights(2,2)
+ input(j,2)*weights(2,3);
x2(2) = 1/(1+exp(-H2));
% Output layer
x3_1 = bias(1,3)*weights(3,1)
+ x2(1)*weights(3,2)
+ x2(2)*weights(3,3);
out(j) = 1/(1+exp(-x3_1));
% Adjust delta values of weights
% For output layer:
% delta(wi) = xi*delta,
% delta = (1-actual output)*(desired output – actual output)
delta3_1 = out(j)*(1-out(j))*(output(j)-out(j));
% Propagate the delta backwards into hidden layers
delta2_1 = x2(1)*(1-x2(1))*weights(3,2)*delta3_1;
delta2_2 = x2(2)*(1-x2(2))*weights(3,3)*delta3_1;
% Add weight changes to original weights
% And use the new weights to repeat process.
% delta weight = coeff*x*delta
for k = 1:3
if k == 1 % Bias cases
weights(1,k) = weights(1,k) + coeff*bias(1,1)*delta2_1;
weights(2,k) = weights(2,k) + coeff*bias(1,2)*delta2_2;
weights(3,k) = weights(3,k) + coeff*bias(1,3)*delta3_1;
else % When k=2 or 3 input cases to neurons
weights(1,k) = weights(1,k) + coeff*input(j,1)*delta2_1;
weights(2,k) = weights(2,k) + coeff*input(j,2)*delta2_2;
weights(3,k) = weights(3,k) + coeff*x2(k-1)*delta3_1;
end
end
end
end
Hopefully someone can help me with this. Thanks.
Berry,
Your ‘out’ variable is converging to [0.5; 0.5; 0.5; 0.5]? I copy and pasted your code, and was getting close to [0; 1; 1; 0]. Not sure what the difference is though…
Can you tell me what your weights end up being? Maybe change the iterations to just 2 or 3 or something small, and then track how the weights and out change over the course of just a couple iterations. The math should be easy to follow using just a couple iterations as well, so you can see where it might be failing.
Sorry its not working out properly. If anyone else has suggestions, we’re all ears.
Vipul
i have looked at this problem and can replicate both using the code above. My understanding is that, sometimes the gradient descent algorithm which is used to find the weights for min error, finds a local minimum in the error function which results in 0.5 / 0.5 / 0.5 / 0.5 rather than the weights for the global min of the error function which for the 0utput 0 / 1 / 1 / 0.
I had the same problem the first time I ran it; check that the equations for H1, H2 and x3_1 fit in one line each; that solved it for me. Thanks a lot for the material, Vitpul!!
Buen aporte
hi
you could be stuck in a local minimum due to your initial / starting points. try to change your initial points to overcome the local minimum solution
I
Thats gorgeous.I facedthe same problem. Just writing H1,H2, and x3_1 equations in one line makes it work.
I faced the same problem. Just writing H1,H2, and x3_1 equations in one line makes it work.
It works. Thanks.
H1 = bias(1,1)*weights(1,1)+ input(j,1)*weights(1,2)+ input(j,2)*weights(1,3);
% x2(1) = 1/(1+exp(-H1));
x2(1) = sigmf(H1,[1 0]);
H2 = bias(1,2)*weights(2,1)+ input(j,1)*weights(2,2)+ input(j,2)*weights(2,3);
% x2(2) = 1/(1+exp(-H2));
x2(2) = sigmf(H2,[1 0]);
% Output layer
x3_1 = bias(1,3)*weights(3,1)+ x2(1)*weights(3,2)+ x2(2)*weights(3,3);
out(j) = sigmf(x3_1,[1 0]);
% out(j) = 1/(1+exp(-x3_1));
out
0.0203837394074010
0.985675210748374
0.979827192504129
0.0208694035914071
weights
3.50037518998636 7.69595389507992 7.88658327304201
-10.0563920494119 -7.28192666154662 -6.20904624184347
12.7628389804905 8.64408359351013 8.63744373236975
Hi,
Why is the equation for calculating H1 (and H2) look different with your network representation in the graphic? Shouldn’t H1 be calculated as H1 = bias(1,1)*weights(1,1) + input(j,1)*weights(1,2) + input(j,2)*weights(2,2)?
And also H2 = bias(1,2)*weights(2,1) + input(j,1)*weights(1,3) + input(j,2)*weights(2,3)?
Of course your code still works, but maybe it’s good for keeping the consistency with your picture.
Hey good catch, i’ll try to fix that when i get a chance.
Did you ever change that?
Find of the day! Great work!
Very helpful.
Thanks
Hi. Nice posting. Thank you very much for this material. I am doing NN for my study. So this is very helpful. Hope you can post more on NN.
The sigma code is a simple function that squashes the data between a certain range. One such sigmoid function example could be something like the following:
function x = sigma(net)
x = 1/(1+exp(-net));
Hi,
thanks for the tutorial, but aren’t you missing the sigma code? I am referring to this in-code comment:
% Note that sigma is a different m file
% that I created to run this operation