While Matlab is known for its capabilities in solving computationally intensive problems, it is also very useful in handling symbolic expressions, and further solving simple algebraic equations. In this tutorial we will investigate how to represent symbolic variables using the functions ‘sym’ and ‘syms’, solve equations using ‘solve’, and plot solutions to these symbolic expressions.

Let’s create our variables. This can be done using either ‘sym’ or ‘syms’. The function ‘sym’ will allow you to create a symbolic variable, with additional arguments specifying whether the object should be ‘positive’,’real’, and in the case of the second argument being a m x n array, will create m x n symbolic variables. ‘Syms’ allows for a shorthand approach for assigning multiple symbolic variables.

>> x = sym('x');
>> y = sym('y');
>> z = sym('z');

or initialize all of them at once:

>> syms x y z;

As a sidenote, ‘sym’ can also be used to represent numbers in their rational form.

>> a = sym(4.12) 
a = 
103/25 

Symbolic variables can further be combined into equations (‘f’). If we want to evaluate these functions, then use a substitute function (‘subs’) to replace the variables with values.

>> f = x + y - z;
>> subs(f,{x y z},{1 2 3})
ans =
     0

We can utilize the symbolic ‘solve’ function to help us evaluate equations.

>> solve('sin(x) = 1')
ans =
pi/2

>> x = solve('2*x-8 = 10')
x =
9

If we have multiple linear equations, with an equal number of unknowns, solve can further be used to solve for each variable. For example we can solve for ‘x’,’y’, and ‘z’ in the following three equations.

>> [x y z] = solve('x+y-z=4','x-2*y+3*z=-6','2*x+3*y+z=7')
x =
1
y =
2 
z =
-1

If you have fewer equations than the number of variables that you are solving for, ‘solve’ can be used to determine the solution to your variables of interest in terms of the remaining free symbolic variable. For example if you have 2 equations, with 3 unknowns, you can solve for 2 variables with respect to the third one.

>> [x y] = solve('x+y-z=4','x-2*y+3*z=-6','x,y')
x = 
2/3 - z/3
y =
(4*z)/3 + 10/3

>> [x z] = solve('x+y-z=4','x-2*y+3*z=-6','x,z')
x =
3/2 - y/4
z =
(3*y)/4 - 5/2

Some other useful symbolic commands that might allow for easier evaluation or computation include ‘expand’, ‘simplify’, and ‘pretty’.

>> syms x y
>> expand(cos(x-y))
ans =
cos(x)*cos(y) + sin(x)*sin(y)

>> simplify(sin(x)^2+tan(x)^2)
ans =
1/cos(x)^2 - cos(x)^2

>> pretty(ans)
     1            2 
  ------- - cos(x) 
        2 
  cos(x)

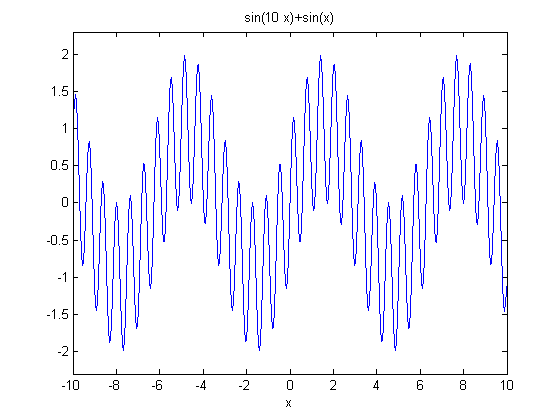
Finally, we can create plots of functions using symbolic variables. If we want to see a 10Hz signal superimposed over a 1Hz signal, over the range of -10 to 10, we can use ezplot to do so.

ezplot('sin(10*x)+sin(x)',[-10 10])

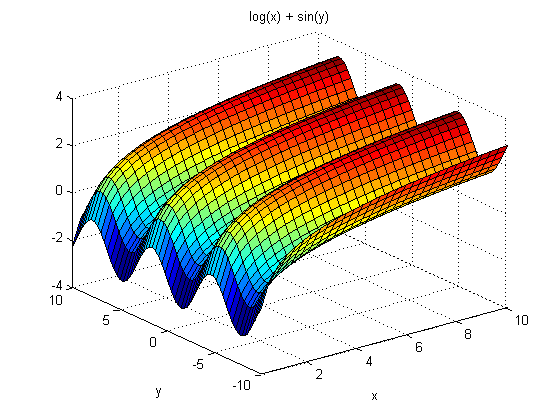
Similarly, using ‘ezsurf’ to create a three dimensional contour plot, we can once again visualize over the range of -10 to 10 in both the x and y direction for a combination of a logarithmic and sinusoidal function.

>> ezsurf('log(x) + sin(y)',[-10 10 -10 10])

As you can see, symbolics allow for a way to evaluate expressions similarly to what you might do in Mathematica (or Maple). Take a look at another post to see how symbolics can be used for simple calculus (derivatives and integration) and compare it to numerical approaches.