Binary classification is the act of discriminating an item into one of two groups based on specified measures or variables. While previously we have discussed methods for determining values of logic gates using neural networks (Part 1 and Part 2), we will begin a series on clustering algorithms that can be performed in Matlab, including the use of k-means clustering and Gaussian Mixture Models. Prior to doing so, we will discuss how classification is evaluated, primarily through the discussion of sensitivity, specificity and the way to calculate these values through Matlab.
In order to properly evaluate a classifier, the outcome of the classifier or test is compared to that of the gold standard. High accuracy is assured when correct classification of members into both groups can be accomplished. For example, lets look at the following example (fake samples) where two clusters are generated based on a person’s height and weight. The goal is to try and determine gender of each individual.
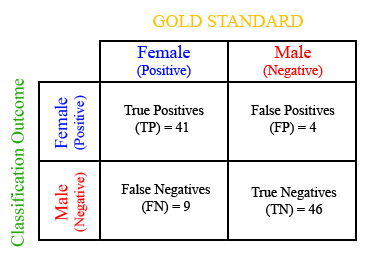
The dots represent a measure’s prediction for classifying an individual as male (red) or female (blue). Circles represent mistakes that were made in classification versus the gold standard. Based on this classification, we can create a contingency table that describes all the different combinations of correct and incorrect classifications.
The terms true positive, true negative refer to the correct identification of females and males (or any test outcome). The terms false negative and false positive refer to the incorrect classification of females and males (or again, any outcome variable). The values for the TP, TN, FP and FN can be derived based on a simple Matlab function written as follows.
function [sens spec ppv npv] = contingency_table(gold,test_outcome) % Where the input gold refers to the gold standard classification % of all individuals with 1s and 2s representing females and males. % test_outcome is the predicted classification of females and males, % again as 1s or 2s. % sens, spec, ppv and npv stand for sensitivity, specificity, % positive predictive value, and negative predictive value % True positives TP = test_outcome(gold == 1); TP = length(TP(TP == 1)); % False positives FP = test_outcome(gold == 2); FP = length(FP(FP == 1)); % False negatives FN = test_outcome(gold == 1); FN = length(FN(FN == 2)); % True negatives TN = test_outcome(gold == 2); TN = length(TN(TN == 2)); % Sensitivity sens = TP/(TP+FN); % Specificity spec = TN/(FP+TN); % Positive predictive value ppv = TP/(TP+FP); % Negative predictive value npv = TN/(FN+TN);
Sensitivity and specificity tells us our ability to properly classify females and males, respectively. In this example, we have 82% (41/50) sensitivity and 92% (46/50) specificity. While the overall goal of any classification scheme is to obtain high accuracy results, as you will see in future tutorials, as the classification threshold is modified, this could affect sensitivity (or specificity) in favor of specificity (or sensitivity). This trade-off between accuracy is often demonstrated through the receiver operating characteristic (ROC) curve.
The next tutorial will demonstrate how to actually utilize clustering techniques to classify individuals into two distinct categories. In order to evaluate performance, we will use the concepts and terms described here.


Hi,
I have two raster images (tiff format) – a flood map and a test image that I want to test using the codes above. My problem is I really do not know to place or load these images in the code. I am really knew to matlab and I would appreciate any expert advice regarding this concern. Thank you very much
I have learned a bit about binary classification but not as exciting and clear as this one! Thanks for sharing!
How exactly do I type in the code in MATLAB to give me the values for FP, FN, TP, and TN?
Hi, I have a problem:
How can I choose and set a threshold for best classification (two classes) on a specific feature with Matlab?
Please explain me the actual codes for TP, TN, FP, & FN…
Thank you!!
TP indicates that we have found the total number of times that the gold standard and the test outcome both have the value ‘1’ in the same location in the array.
TN is similar to TP, but instead we have found when gold and test_outcome both have ‘2’ in the same location in array.
FP and FN look for the number of times that a row in gold vs a row in test_outcome disagree.
Marco,
Good questions. I’ll try to modify the post to include some of your comments.
The test_outcome and gold variables would be a vector of values (n x 1), where n is the number of subjects. Each cell in the vector would contain the value 1 or 2, depending on whether the person is female or male.
The lines:
TP = test_outcome(gold == 1);
TP = length(TP(TP == 1));
allow us to count the number of persons we correctly identified to be 1, when comparing the test_outcome to the gold standard. Try running the code on a simple array like gold = [1; 2; 1; 1; 2;] and test_outcome = [1; 2; 2; 1; 1] to see what values you get for TP, FP, etc.
Sensitivity tells you the percent accuracy based on the number of true positives out of the total number of subjects that are actually female (positive). So looking at the contingency table that would be 41/50, where 41 = TP and 50 = TP + FN. The same is true for specificity, where in this case the number of males accurately identified out of all actual males is calculated.
Hope this helps. Take care,
Vipul
Thank you for having a nice tutorial in binary classification.
Would you mind providing the actual set of code also? I’m new to MATLAB and am kind of confuse about how some code above actually works. For example:
TP = test_outcome(gold == 1);
TP = length(TP(TP == 1));
I wonder how “test_outcome” and “gold” actually look like.
Also, could you explain a little bit more how you determine “sens” equals “TP/(TP+FN)” and “spec” equals “TN/(FP+TN)”?
Thank you very much!