Polynomial curve fitting is a common task for data analysts in many fields of science, engineering and social science.  The standard method to fit a curve to data is to use the least squares method.  In this method, the coefficients of the estimated polynomial are determined by minimizing the squares of errors between the data points and fitted curve.  This method is used to determine the relationship between an independent and dependent variable.  The common term regression line is used for a first-degree polynomial.  Matlab has a simple function called polyfit that allows an analyst to use the least squares method.  In this post, a simple example of polyfit is presented to determine the relationship between two variables in a noisy environment.

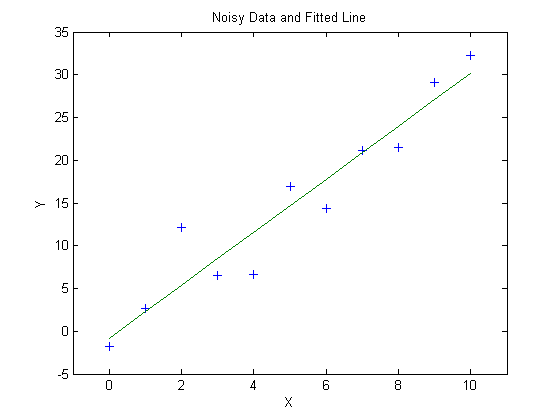The above plot shows a set of data and the fitted line created by polyfit.  The linear relationship between the two variables is obscured by Gaussian noise.  However, even with noise of moderate variance, polyfit estimates that the equation that describes the relationship between the data is

y = 3.0959x – 0.796

This result is not far off from the real equation, which is

y = 3x

The following code is used to create the plot in this post.  The function polyfit calculates the coefficients of the fitted polynomial, and the function polyval determines the values of that polynomial at the desired data points.  To use a polynomial of a higher degree to fit the data, just change the third parameter of polyfit to the degree of the polynomial.

x = [0:10];   %Dependent variable

y = 3*x + 4*randn(size(x));    %Independent variable

%Find estimated polynomial
p = polyfit(x,y,1);   

%Find values of estimated polynomial on values of X
poly_line = polyval(p, x);  

%Plot data and estimated polynomial
figure
hold all
plot(x,y,'+')
plot(x,poly_line)
xlim([-1 11])
xlabel('X')
ylabel('Y')
title('Noisy Data and Fitted Line')
box